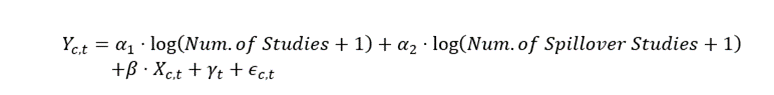Abe Dunn and Lasanthi Fernando, Bureau of Economic Analysis, U.S. Department of Commerce, and Eli Liebman, Terry College of Business, University of Georgia
Contact: eli.liebman@uga.edu
Abstract
What is the message? The authors provide new evidence for the broadly held view that medical innovation is a key driver of spending growth. Through the development of proxy measures of innovation for specific conditions, they show that conditions targeted by more cost-effectiveness studies are conducted, experience significantly more spending growth.
What is the evidence? A database on cost-effectiveness studies from the Tufts Cost-Effectiveness Analysis Registry (CEAR), and cost-effectiveness studies and data on spending growth at the condition level from the Bureau of Economic Analysis (BEA) Health Care Satellite Account (HCSA).
Timeline: Submitted: June 10, 2023; accepted after review Sept. 1, 2023.
Cite as: Abe Dunn, Lasanthi Fernando, Eli Liebman. 2023. A Direct Measure of Medical Innovation on Health Care Spending: A Condition-Specific Approach. Health Management, Policy and Innovation (www.HMPI.org), Volume 8, Issue 2.
We would like to thank Calvin Ackley, Dennis Fixler, and Justine Mallatt for comments. The views expressed in this paper are those of the authors and do not necessarily represent the US Bureau of Economic Analysis, or the US Department of Commerce.
Introduction
There is a large amount of literature that explores the connection between innovations and healthcare spending (Chernew and Newhouse (2011)). Understanding the effects of innovation in driving expenditure growth is important, as growth in spending due to innovation may reflect improvement in patient care and welfare, rather than inflation, inefficiency, or a less healthy population. Healthcare innovation has historically been difficult to measure as there are hundreds, if not thousands, of unique conditions and even more treatments that evolve over time. A common approach to measure the effects of technology on spending is to examine a few specific case studies, though applying this approach to all new technologies is extremely difficult (See Chernew and Newhouse (2011) for a review). An alternative approach is to control for measurable drivers of spending (e.g., aging of the population, changing insurance coverage, changing prices, and rising incomes), where growth in spending that cannot be explained by these known factors is assumed to be driven by innovation (Schwartz (1987), Newhouse (1992), Cutler (1995), Smith et al. (2009)), and Smith et al. (2022)).[1] This approach is referred to as the residual approach, as innovation is measured as the spending growth that cannot be explained by other factors, similar to Solow (1957). A limitation of this approach is that other factors such as market power, inefficiency, or changes in the health system organizations, may also enter the residual, which would contaminate the contribution of medical innovation.
This paper takes a unique approach to this measurement challenge. Specifically, we use a comprehensive database on cost-effectiveness studies from the Tufts Cost-Effectiveness Analysis Registry (CEAR) to proxy for the level of innovation by condition. Cost-effectiveness studies are a well-suited proxy for innovation as they capture entry of new treatments or exploration of treatments for distinct populations. This contrasts with other indicators of innovation, such as patents, which may not represent innovations that are fully developed or even applicable in practice.
To connect the cost-effectiveness data to information on population spending, we use data from the Bureau of Economic Analysis’ (BEA) Health Care Satellite Account (HCSA) for the years 2000-2017. The HCSA is a unique account of national health care spending that decomposes health care spending by condition (e.g., diabetes, heart attacks) rather than by type of service (e.g., physician offices, hospitals, or prescription drugs) as is done in the Centers for Medicare and Medicaid Services’ (CMS) National Health Expenditure Account (NHEA). This distinction is important as technologies are typically applied to specific conditions.
We connect HCSA’s information on spending at the condition level to information on cost-effectiveness studies for the associated condition category. The effect of technology is identified by cross-condition correlations in the relative growth rates in spending and the number of innovations, while controlling for a variety of factors. Importantly, we include year fixed-effects that account for all common factors that might affect spending growth across conditions. For example, if hospital or physician consolidation affects the treatment of many conditions, it would be picked up in the year fixed effect.
We find a significant relationship between the number of studies and the rate of spending growth by condition, providing unique evidence consistent with the theory that innovation drives spending growth. We find that innovation accounts for about 18 percent of the total growth in spending per capita (after accounting for economy-wide inflation), but our estimates range from 13 to 32 percent. These estimates are slightly lower than recent residual-based studies that suggest innovation accounts for between 25 and 50 percent of the growth rate in spending. (Smith et al. (2009) and Smith et al. (2022)).2 We argue that the 18 percent contribution to spending growth is likely a lower bound on the actual impact of innovation on spending for a couple of reasons.
First, the number of studies is an imperfect proxy for innovation, which could lead to some attenuation in the estimate. Second, some innovations are common across many conditions, which would not be captured by our estimates, which are based on relative growth rates across conditions.3
The results are robust across a number of alternative specifications, such as controlling for demographic changes, controlling for 18 broader disease category trends (e.g., circulatory conditions or cancers), the spending level of the condition, and the initial spending growth of the condition. We also run alternative estimates where we normalize the number of cost-effectiveness studies across years to account for an overall growth in cost-effectiveness studies in the literature. Finally, using alternative proxies of innovation by condition, such as the change in quality of treatments estimated from the cost-effectiveness studies, we still find a significant and positive relationship between spending growth and these alternative proxies. Across all of these specifications, we find a strong relationship between measures of innovation and spending growth.
We also investigate whether innovation affects spending through growth in treated prevalence or in spending per case. The expected result is not clear because some innovations may be expensive, while others may be cost-saving or allow for substitution away from costlier services. For example, less invasive surgical techniques may reduce spending per case, but could increase overall costs if they cause individuals to seek medical care for previously untreated conditions. We find no correlation between our proxy for innovation and spending per case or treated prevalence. More likely, the effect is idiosyncratic to each condition and the effect could be highly dependent on the type of technology. Indeed, Cutler et al. (2022) find that medical spending trajectory varies greatly by medical condition, and this partly depends on the type of technologies that diffuse (e.g., low cost or high cost technologies).
Validating this idea, we do find that the relative cost of new innovations, as reflected in the CEAR cost-effectiveness database, is significantly related to observed changes in spending growth by condition, where this effect occurs through spending per case, and not through treated prevalence. In other words, when technologies appear costly in the CEAR database, this does seem to be reflected in a higher spending per case in the HCSA.
The findings in this paper have important implications for economic measurement including measures of price, output and productivity. If spending is primarily driven by non- technological factors, then traditional price measures are well-suited to measure output and productivity for the sector. However, if spending is driven by innovation, then traditional measures will not accurately reflect consumer welfare changes (Dynan and Sheiner (2018)). While it is commonly believed that innovation is a key driver of health care spending growth, most of the evidence is based on empirical studies that make strong assumptions regarding the unexplained health care spending growth. This paper provides unique evidence, applying alternative assumptions and methods, and similarly concludes that innovation is a significant driver of spending growth. This is especially important for the pharmaceutical sector, which account for about 44 percent of the studies in our CEAR database. This reinforces the importance of exploring alternative measures of price, output and productivity for the health care sector (see Cutler et al. (2022), Highfill and Bernstein (2019), Weaver et al. (2022), Romley et al. (2020), Eggleston et al. (2019), Dunn et al. (2022), and Matsumoto et al. (2021)), despite the fact that the measurement issues in health care are challenging (Sheiner and Malinovskaya (2016), Hall (2017), and Dauda et al. (2022)).
Materials and Methods
This paper uses two main data sources. One data source is the Cost-Effectiveness Analysis Registry (CEAR) from the Tufts Medical Center. The registry gathers published cost-
effectiveness studies and extracts information on: the intervention (innovation), the control (often a standard of care treatment), outcomes measured in Quality Adjusted Life Years (QALYs)4, and associated costs of the treatments. The version of the registry used in this study contains over 7,000 cost-effectiveness studies published since 1976. The registry aims to be a comprehensive source of cost-effectiveness studies, excluding only studies that are not published in English and those that do not measure outcomes in QALYs. We drop articles that were missing disease information, missing QALY information, or outside our sample period. In total, our sample includes 4,766 articles.5 While the CEAR database covers all types of innovations, innovations in the pharmaceutical sector are especially important and account for 44 percent of the observations in the CEAR database.
The second data source is from the BEA’s Health Care Satellite Account (HCSA) (Dunn et al. (2015) and Dunn et al. (2018)). The account combines large health care claims data, amounting to millions of patients and billions of claims, to report a representative estimate of spending by disease for the entire U.S. population. Using the HCSA data, we construct measures of the 5-year per capita growth rate of spending, spending per case, and treated prevalence.6 We use the years 2000-2017, but because of a change in disease coding after 2015 (from ICD-9 to ICD-10 disease classification) there is a discontinuity between 2015 and 2016. Therefore, our main analysis focuses on the years 2000-2015, and we examine the full period 2000-2017 as a robustness exercise in the appendix. All estimates are reported in 2017 dollars by applying the GDP price index.
The main dependent variable is the 5-year growth rate in spending per capita. We focus primarily on 5-year growth rates as it may take time for technologies to diffuse and impact spending. Because we measure 5-year growth rates, our main regressions will include the years 2005-2015.
The main variable of interest is the number of studies for a given condition. To account for the diffusion period, our measure of the number of studies is the lag of the number of studies over the past five years for that condition category. For instance, for hypertension in the year 2015, we look at the total number of studies related to treatments of hypertension over the previous 5 years (2010-2014).
Although the condition categories reported in the Tufts registry do not correspond precisely to the 260 Clinical Classification Software (CCS) categories reported in the HCSA, we construct a mapping at the most detailed level possible, with the understanding that the mapping may be imperfect. We map the conditions two ways. First, the Tufts’ “Disease or Health Intervention” variable was manually mapped to CCS categories based on the text re- ported in the cost effectiveness study (e.g., “Disease or Health Intervention=Hypertension” was manually mapped to both CCS=98 (Hypertension), and CCS=99 (Hypertension with complications)). Second, we mapped the Tufts data to CCS categories using their listed 3- digit ICD-10 codes. Subsequently, the CCS mappings between the two methodologies were compared for equivalency. There were 3,142 articles where the manual mapping and map- ping based on the 3-digit ICD-10 codes agreed on a single CCS category. For the remaining 1,624 articles where there was a disagreement in the mapping, the CCS category with the larger average spending over the (2000-17) period was assigned.7
As the mapping between the Tufts disease conditions and the CCS categories may be imperfect and technological innovations may spillover to related conditions, we use a broader disease classification that categorizes the 260 conditions into more encompassing 64 Agency for Healthcare Research and Quality (AHRQ) categories (e.g., CCS=Breast Cancer, and CCS=Lung Cancer would both map to AHRQ=Cancers). Using these broader 64 categories, we create a variable of spillover studies, where we look at the average number of studies for other conditions in the broader category over the past five years. The higher this value, the more studies there are on related conditions.8
In addition to the number of studies, we also explore alternative proxies of innovation by looking at measures of quality in the cost-effectiveness studies. In particular, we measure the median difference in QALYs (between the intervention and the comparator) from innovations by condition in each year. We then average the difference in QALYs across years. We similarly examine incremental cost differences between innovative and comparative treatments. As we do not have measures of the importance of these individual innovations nor how the associated technologies diffuse, these additional measures should also be viewed as proxies of innovation and cost changes related to innovation.
Descriptive Statistics
Table 1 displays total spending and total number of research studies over the entire sample period from 2000-2017 by 18 broad disease categories. In general, the categories with the most spending also have a higher number of research studies. However, there is a lot of heterogeneity in the number of studies and total spending. Neoplasms, which includes cancer, contains the largest number of studies, but does not account for the largest expenditures. In contrast, the symptoms category, which primarily includes preventative services such as routine checkups, accounts for a large share of spending, but observes very few studies in this category.9 These broad condition categories are useful for summary purposes but are too broad to look at the relationship between innovation and spending growth. Headache and glaucoma both fall under the category of “diseases of the nervous system,” but the technologies to treat these two conditions are distinct. For this reason, we focus our analysis on the more disaggregated CCS condition categories, that include 260 conditions, but allow for some technological spillover by also looking at 64 broader AHRQ condition categories.
Table 1: Total Spending and Count of Research Studies by Broad Condition Category
| Dollars (Bil) | Num of Studies | |
| Circulatory conditions (e.g., hypertension) | 3,842.3 | 717 |
| Routine care, signs and symptoms (e.g., preventative care) | 3,579.5 | 16 |
| Musculoskeletal conditions (e.g., back problems and arthritis) | 2,795.2 | 479 |
| Respiratory conditions (e.g., COPD and asthma) | 2,478.5 | 259 |
| Nervous system conditions (e.g., cataracts and epilepsy) | 2,088.4 | 276 |
| Endocrine system conditions (e.g., diabetes and high cholesterol) | 1,922.1 | 436 |
| Injury and poisoning (e.g., trauma) | 1,880 | 151 |
| Neoplasms (e.g., cancers and tumors) | 1,879.8 | 1,013 |
| Genitourinary conditions (e.g., kidney and reproductive diseases) | 1,747.9 | 190 |
| Digestive conditions (e.g., gastrointestinal disorders and appendicitis) | 1,611.4 | 198 |
| Mental illness (e.g., depression and dementia) | 1,290.8 | 295 |
| Infectious diseases (e.g., septicemia and HIV) | 1,176 | 554 |
| Skin conditions (e.g., acne and infections) | 714.5 | 57 |
| Pregnancy (e.g., deliveries and contraceptives) | 668.9 | 19 |
| Residual codes; unclassified; | 569.5 | 56 |
| Blood disorders (e.g., anemia) | 340.4 | 24 |
| Perinatal conditions (e.g., low birth weight) | 126.9 | 11 |
| Congenital anomalies (e.g., cardiac anomalies) | 124.1 | 15 |
| Total | 28,836 | 4,766 |
Note: This table shows total spending in the HCSA scaled to match the National Income and Product Accounts (NIPA) estimates of health care spending, and total number of studies using the CEAR by broad disease category, covering the years 2000 to 2017.
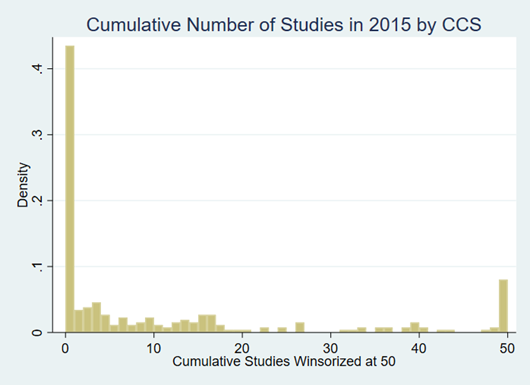
For the 260 condition categories there is a lot of heterogeneity in the number of studies we see per condition in any 5-year span. Figure 1 shows the distribution of the number of studies by CCS category for 5 years prior to 2015. The distribution shows that a little over 40 percent of conditions have no studies. There is a skewed distribution of the number of studies across conditions, where we have winsorized the histogram at 50. This shows a wide distribution in the number of studies observed.
Figure 1: Density of Number of Studies in CCS Category over the Past 5 Years
Notes: This figure shows the cumulative distribution for the cumulative number of studies across the 260 CCS categories in 2015. The figure shows that over 40 percent of the categories have no associated cost- effectiveness studies. The number of studies for a particular category is highly skewed. The figure shows a mass point on 50 because we winsorized the distribution at 50.
Next, we turn to variation in spending growth. Figure 2 graphs the ten of the condition categories which had the largest average spending (level) per capita over the period of study. We also include hepatitis and cystic fibrosis, two conditions with substantial research and improvements in treatment over the past couple of decades. The figure demonstrates that there is wide variation in spending trends. It is this difference in spending growth rates and number of studies across conditions that will help identify the effect on spending variation.
Figure 2: Spending Growth Per Capita Trends for 12 Conditions
Notes: This figure shows spending trends for the 12 CCS conditions, adjusted for economy-wide inflation. The twelve conditions reported in order of average level of spending include: medical exam/evaluation; spondylosis; hypertension; other connective tissue; residual codes; other screening; coronary atherosclerosis; diabetes without complication; other non-traumatic joint disorder; rehabilitation care; hepatitis; and cystic fibrosis. The first 10 were selected because they had the highest average spending per capita over this time period, while hepatitis and cystic fibrosis are known to have major technological advances over this period. Only five of the conditions are labeled in the figure and were selected as they are more easily recognizable. Spending has been deflated to 2017 dollars using the GDP price index from BEA. The figure demonstrates a wide range in variation in spending trends by condition.
While there is considerable variation in the number of studies and spending growth, the goal of this paper is to see how those correlate. The top ten conditions in terms of spending growth (in percentage terms) include conditions with substantial innovation. These include cystic fibrosis, hepatitis C (graphed above), and multiple sclerosis. Cystic fibrosis has had breakthrough innovations such as Kalydeco®, Orkambi®, Symdeko®, Trikafta®), costing anywhere between $100,000 – $350,000 a year (Tice et al. (2020)). For multiple sclerosis, breakthroughs in the development of monoclonal antibody therapies have led to drugs such as Tysabri®, Ocrevus®, Kesimpta®, Campath®, and Leustatin® being approved since 2004 (Olek and Mowry (2022)). For hepatitis C, in 2014, the launch of Sovaldi®, sparked public uproar as it crowned itself the costliest drug for the Medicare program, totaling $94,000 a year (or $4.5 billion in a single year for Medicare) (Olek and Mowry (2015)). While these examples suggest that innovation is driving some spending growth, our goal is to determine the correlation across all conditions.
Table 2 provides some descriptive statistics that hint at the main result in this paper. The columns in Table 2 show descriptive statistics for key variables broken out in each panel based on the number of studies observed. The first panel includes observations where there are zero studies observed for the corresponding CCS condition category for the past 5 years; the second panel provides the descriptive statistics for CCS categories with between one to five studies; and the third panel provides descriptive statistics for conditions where there are more than five studies over the past five years. The descriptive statistics show that the mean spending growth rate for CCS categories grows faster for condition categories where there is one to five studies (growing at 14.3 percent over a 5-year period) versus conditions where there are no associated studies (growing just 8.9 percent per year). The next column reports the average difference in QALYs (between the intervention and comparator) per study, where the value is set to zero if there are no studies. The average QALY difference when there is between one to five studies is large, 0.47, but it is highly skewed, with the median gain in QALYs of 0.07. The average difference in QALYs highlights that these studies are typically associated with improvements in treatment quality, although the exact diffusion and importance of these QALY gains is not observed.10
Table 2: Descriptive Statistics by Number of Studies in the Past Five Years
| Spend Growth | Num. of Studies | Avg. Growth QALY | Num. of Spill. Studies | |
| Zero Studies | ||||
| mean | 0.0894 | 0 | 0 | 2.972 |
| p50 | 0.0600 | 0 | 0 | 1.412 |
| sd | 0.237 | 0 | 0 | 4.030 |
| count | 1575 | 1575 | 1575 | 1575 |
| One to Five Studies | ||||
| mean | 0.143 | 2.458 | 0.478 | 4.280 |
| p50 | 0.0957 | 2 | 0.0700 | 2.155 |
| sd | 0.257 | 1.386 | 0.849 | 7.696 |
| count | 740 | 740 | 740 | 740 |
| More than Five Studies | ||||
| mean | 0.141 | 18.14 | 0.336 | 5.143 |
| p50 | 0.105 | 13 | 0.166 | 3.500 |
| sd | 0.238 | 16.63 | 0.483 | 9.031 |
| count | 553 | 553 | 553 | 553 |
Note: This table shows descriptive statistics based on the number of studies in a CCS category over the past five years. The three categories capture the number of studies over the past five years, where the categories are zero, one to five, or more than five research studies. The table shows that the growth rates in spending at the mean and median are lower for those condition categories that have no research studies, compared to those categories that have between one and five or more than five. These estimates exclude outlier five-year growth rates that are above 200 percent, which are also removed from our regression analysis.
The statistics in Table 2 also suggests that multivariate analysis may be important for a few reasons. First, there is a lot of variation in the spending growth rate, as reflected in the standard deviation, so it may be important to include additional controls, such as year fixed effects that would account for overall medical care inflation, and other common factors affecting the growth rate across conditions. Second, there is a lot of variation in the number of spillover studies, so it may be important to account for this additional proxy of innovation for each condition. For example, for the zero-studies category, the average number of spillover studies is around 3.
Analytical Framework
The regression takes the following functional form:
The variable Yc,t is the growth rate over the past five years in per capita spending, for condition c in year t. To measure how the number of studies over the prior five years is related to spending growth, the main covariates are log(Num. of Studies + 1) and log(Num. of Spillover Studies + 1). In other words, equation 1 is testing whether growth rates are faster for those CCS conditions or AHRQ condition groups where we observe more associated cost-effectiveness studies. For example, there have been many studies for hepatitis, and we observe subsequent rapid spending growth. We focus on a simple count on the number of studies rather than QALYs or costs observed in the cost-effectiveness studies for a few reasons. First, there is a lot of heterogeneity in the measurement of costs and QALYs across studies, for example the assumptions made or populations used can vary considerably. Second, innovations can impact costs and QALYs in heterogeneous ways, making them noisy measures of “innovation.” For example, a new drug that cheaply replaces a high-cost procedure with slightly worse outcomes may reduce QALYs and costs. Meanwhile, a highly effective but expensive new drug may increase both costs and QALYs. Both of these may represent innovations which improve welfare, but their impact on costs and QALYs may cancel out.
We include covariates to account for potential confounding factors. Arguably the most important variable is the year fixed effects, γt, which captures the aggregate growth rate that is common across all conditions. The γt control distinguishes our analysis from other work in the literature because it accounts for numerous common factors that could influence the aggregate growth in spending such as changes in income, medical inflation, insurance and other factors that affect spending on multiple conditions that are common across conditions. This differs from other work in the literature that attempts to control for these factors using only aggregate data, which requires strong assumptions regarding factors affecting aggregate growth rates in the medical care sector. In those studies, growth due to changes in market power or inefficiency in the health care sector may be difficult to control for and enter the aggregate residual, along with the effects of technological change. In contrast, we are using cross-condition variation controlling for many of these aggregate trends using year fixed effects.
Although the Tufts CEAR data is comprehensive and includes studies from the 1970’s, the number of cost-effectiveness studies increased substantially over time, with about 95 percent of the studies appearing over the 2000-2015 period. Because we include year fixed effects, the growth in the number of studies has little effect on the estimates, as we are measuring the effect on the relative growth rates across conditions. However, we also include a robustness check where we normalize the number of studies in each year.
The term, Xc,t, includes additional controls that might have differential effects on the growth rate of each condition. We include predicted spending growth based on demographic changes, by condition, described in more detail below. In some specifications we also include the initial annual spending per capita of the condition, the initial spending per case of that condition, broad condition category trends (the condition categorization with 18 categories as in Table 1), and the initial 3-year growth rate in spending for the condition. The error term in the equation is ϵ_(c,t).
One variable that may be unique to each condition is demographic factors such as age and sex. For instance, the aging of the population may have a larger effect on circulatory conditions, relative to conditions related to pregnancy. Adding an age variable directly into our regression model for each condition is not possible because there would be too many covariates (e.g., average population age interacted with each condition category). Instead, we use the Medical Expenditure Panel Survey (MEPS) to measure spending by each age and sex group for each condition. The MEPS has a relatively small sample size (around 30,000 individuals), but we combine 19 years (2001-2019) of the MEPS data to estimate average spending for each age-sex category by condition, where the average does not vary over time.11 We use the change in the population age-sex demographics to predict spending growth for each condition based on demographic changes alone (see appendix section A.1.1 for additional details). We include this predicted change in spending due to demographics as a control in our main regression specification.
Our main analysis includes the years 2000-2015, and estimates are clustered by CCS condition category. We get similar results if we select specific years spaced out in 5-year increments (i.e., 2005, 2010, and 2015). We also report results using the full sample from 2000-2017 in the appendix.
Results and Implications
Regression Results
The results of the regression analysis are shown in Table 3. The first panel shows the relationship between spending growth and a single proxy for innovation: the log of the number of studies. The specifications differ across columns, as described in the top row of the table. The first baseline model in the first column includes year fixed effects and the demographic control. The relationship is positive and statistically significant, with an elasticity implying that a 10 percent increase in the number of studies would lead to a 0.2 percent faster spending growth over a 5-year period. The second column removes the demographic control. The third column includes the demographic control and adds additional controls for the amount of spending in the CCS category and includes 18 broad condition category trends. The fourth column is the same as the third column but includes the initial three-year growth rate in spending for the condition.12 The fifth column applies an instrumental variable (IV) to the log of the number of studies to account for potential measurement error in our proxy for innovation, which may create attenuation bias. The instruments we apply are alternative measures of innovation from the CEAR database using incremental QALY measures over the past five years, which is not necessarily associated with the number of studies. The sixth column is the same as the baseline but is weighted by the log of spending by condition.13 The estimates are positive and significant across specifications.
The second panel of estimates is the same as the first panel, but includes two proxies for innovation, including the number of studies, and also spillover effects from other conditions in the same AHRQ condition category. We find a positive relationship on both variables across specifications, although the spillover effect loses statistical significance as additional controls are added (column 3). The third and fourth panels of estimates are the same as the first and second, but the number of studies is normalized to be the same across years. The results are qualitatively the same as those in the first two panels, but the standard errors are slightly smaller.14
Table 3: Regression of 5-Year Spending Growth Rates on Counts of the Number of Studies and Studies in Related Categories: Alternative Specifications using Full Sample
| Model Description | Baseline | No Demo. | Controls | Cont. & Trend | IV | Weighted |
|
Single Proxy |
||||||
| Spend | Spend | Spend | Spend | Spend | Spend | |
| Log(Num Studies+1) | 0.0233∗∗ | 0.0232∗∗ | 0.0254∗∗ | 0.0129 | 0.0552∗∗∗ | 0.0223∗∗ |
| (0.00970) | (0.00944) | (0.0111) | (0.00935) | (0.0144) | (0.00967) | |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.021 | 0.022 | 0.119 | 0.245 | 0.003 | 0.023 |
| Two Proxies | ||||||
| Log(Num Studies+1) | 0.0224∗∗ | 0.0212∗∗ | 0.0275∗∗ | 0.0148∗∗∗ | 0.0531∗∗∗ | 0.0216∗∗ |
| (0.00961) | (0.00930) | (0.0115) | (0.00482) | (0.0144) | (0.00960) | |
| Other Log(Num | 0.0237∗ | 0.0221∗ | 0.0204 | 0.0179∗∗∗ | 0.0219∗ | 0.0231∗ |
| Studies+1) | (0.0122) | (0.0114) | (0.0146) | (0.00665) | (0.0124) | (0.0122) |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.027 | 0.027 | 0.121 | 0.247 | 0.010 | 0.029 |
| Single Proxy – Normalized | ||||||
| Log(Num Studies+1) | 0.0217∗∗∗ | 0.0216∗∗∗ | 0.0250∗∗∗ | 0.0137∗ | 0.0324∗∗ | 0.0209∗∗ |
| (0.00831) | (0.00811) | (0.00953) | (0.00772) | (0.0130) | (0.00830) | |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.023 | 0.024 | 0.122 | 0.246 | 0.021 | 0.025 |
|
Two Proxies – Normalized |
||||||
| Log(Num Studies+1) | 0.0211∗∗ | 0.0198∗∗ | 0.0278∗∗∗ | 0.0161∗∗∗ | 0.0304∗∗ | 0.0205∗∗ |
| (0.00825) | (0.00800) | (0.00980) | (0.00408) | (0.0136) | (0.00826) | |
| Other Log(Num | 0.0238∗∗ | 0.0220∗∗ | 0.0245∗ | 0.0210∗∗∗ | 0.0235∗∗ | 0.0233∗∗ |
| Studies+1) | (0.0104) | (0.00970) | (0.0130) | (0.00564) | (0.0104) | (0.0103) |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.032 | 0.032 | 0.127 | 0.249 | 0.030 | 0.033 |
Note: The table shows results from regressions of spending growth per capita on proxies of innovation based on the counts of the number of studies. All regressions include year fixed effects. The columns differ by the covariates included in the specification, with a description in the top column. The baseline specification includes the demographic covariate, second column excludes the demographic covariate, the third column includes additional controls, and the fourth column includes additional controls and the initial 3-year growth rate of the condition. The fifth column applies an IV estimation, where the IV is the average QALY from cost-effectiveness studies over the past five years. The sixth column is the baseline model where the regression is weighted by the log of the average spending. The specification also differs by panel. The first panel includes a single proxy for innovation (log number of studies) and the second panel includes two proxies (log number of spillover studies). The last two panels repeat the first two panel, but the number of studies is normalized across years. Standard errors are in parentheses and are clustered by CCS Condition Category.
Implications
The regression estimates show a strong positive relationship between our innovation proxies and the rate of spending growth. To determine the share of the spending growth attributable to innovations, we compare the observed growth rates to counterfactual growth rates where the number of cost-effectiveness studies is set to zero. Specifically, after estimating equation (1) we compute the counterfactual growth rate if no innovation occurred as reflected by zero cost-effectiveness studies:
Using the alternative growth rate calculated from equation (2) we then recompute the aggregate counterfactual growth rate over the entire period, from 2000 to 2015. An implicit assumption of this counterfactual is that innovation only affects spending growth of conditions that have a positive number of studies or spillover studies.
Table 4 shows the results of this analysis under a variety of different assumptions following the results in Table 3. The top of the table describes the components of the growth rate. The spending per capita was $4,409 in 2000 and grew to $6,911 in 2015, where all values are in 2017 dollars. This translates into a total growth of $2,502, or a 3.0 percent growth rate on an annual basis. The bottom of Table 4 calculates the share of this growth attributable to our proxies for innovation across a variety of scenarios. For each scenario we report the analysis that directly uses the number of studies, but also a secondary analysis where the number of studies is normalized to account for overall trends in the number of studies, as discussed previously. The baseline scenario applies the regression results reported in column (1) of the second panel of Table 3. The estimates show 18.4 percent of the growth is attributable to the innovation proxy. A similar result is obtained when we normalize the proxy for innovation, shown in column (2) of Table 4, where we find that about 17.2 percent of the growth is attributable to proxies for innovation.
Next, we conduct the same calculation, but using the alternative specifications in Table 3. In the second scenario we remove our demographic control; in the third we add additional controls; in the fourth we include the additional controls and the initial trend in spending for each condition; in the fifth we apply IV for the number of studies; and in the sixth we apply weights. In each case, we also conduct these calculations with a normalized innovation proxy, which adjusts for the number of cost-effectiveness studies increasing over time. We consistently find that innovation accounts for a significant fraction of spending growth, ranging from 12.9 to 31.8 percent of the total growth over the 2000 to 2015 period.
Table 4: Share of Spending Growth Attributable to Innovation Based on Number of Studies as Proxy for Innovation
| (in 2017 Dollars) | ||
| Spending Per Capita in 2000 | 4,409 | |
| Spending Per Capita in 2015 | 6,911 | |
| Growth in Spending Per Capita 2000-15 | 2,502 | |
| Annual Growth Rate in Spending Per Capita | 3.0 % | |
|
Share of Spending Growth Attributable to: |
||
| Scenarios | Innovation Proxy | Normalized Innovation Proxy |
| 1. Baseline | 0.184 | 0.172 |
| 2. with No Demographics | 0.173 | 0.160 |
| 3. with Additional Controls | 0.196 | 0.203 |
| 4. with Additional Controls and Initial Trend | 0.129 | 0.141 |
| 5. with IV for Num. of Studies | 0.318 | 0.211 |
| 6. with Basic Controls and Weights | 0.178 | 0.167 |
Note: All spending growth is adjusted for economy-wide inflation using the GDP index. The table shows the contribution of technology to spending growth by calculating the hypothetical spending growth rate assuming the number of cost-effectiveness studies is set to zero. The first column uses the regressions where the actual number of studies are used, while the second column normalizes the total number of studies across years, to account for the fact that the CEAR database is growing substantially over time. The scenarios correspond to the regression results in Table 3 and include: (1) baseline model with demographic control; (2) same as (1), but without demographic control; (3) same as (1) but with broad disease chapter fixed effects, as well as spending per capita and spending per case in the initial year; (4) same as (3) but includes a control for the growth rate for the initial 3 years; (5) baseline estimate with IV applied; and (6) same as (1) but weights based on the log of the spending by disease, so that the larger spending categories count more.
Mechanisms
While the residual approach necessarily takes a broad view of innovation – it is capturing otherwise unexplained factors – the literature on innovation in medical spending more broadly has paid particular attention to how innovation impacts spending and the quality of care. First, it is unclear whether new innovations will improve the quality of care. For example, there is a lot of interest in “follow-on”, “me-too”, and “ever-greening” drugs, which allow manufacturers to capture rents but do not improve patient welfare (Curtiss (2005), Hemphill and Sampat (2012), Fojo et al. (2014), Tabernero (2015), Gastala et al. (2016), and van der Gronde et al. (2017) ). Second, innovations may not necessarily increase costs. For example, a new drug that reduces the number of doctor visits may reduce costs (Ridker et al. (2008) and Giugliano et al. (2020) ). Finally, if an innovation allows treatments of otherwise untreatable conditions or populations (or with fewer side-effects) it could increase the number of people treated without increasing the spending per case (Chernew et al. (1997) and Chernew and Newhouse (2011)). In this section, we explore these different mechanisms.
Role of Cost and QALY Differences
The main analysis uses the number of studies as a proxy for innovation. We focus on the number of studies as it is easily measured and can be normalized to account for the growth in the number of studies over time. However, the cost-effectiveness database can be used to form alternative proxies. The theoretical reason that new innovations drive spending higher is related to both the high costs from new innovations, which often cost more than prior treatments, and the higher quality from innovations, which drive demand for new treatments. In this section we look more directly at measures of costs and quality from the cost-effectiveness studies to see if we can identify some expected patterns.
The cost measure in the CEAR database is the average incremental cost of innovations relative to the comparison treatment in the database over the past five years. For the measure of quality, we use the average incremental QALYs of innovations relative to the comparison treatment over the past five years. If innovations are distinct, we might think the QALYs and costs are additive, so we also compute the total QALYs and total costs across studies. As the proxies are imperfect, we enter them in different combinations in our baseline regression model to investigate correlations.
Table 5 uses the baseline specification and examines how these variables relate to spending growth. Column (1) repeats our main specification using the number of studies. Column
(2) removes the log(Num. Studies + 1) as a covariate and includes the average QALY. We see that a direct measure of QALYs is significantly related to spending growth. Column (3) includes both log(Num. Studies + 1) and the average QALY change. The average QALY change is still positive, but insignificant, likely due to collinearity between QALY change and the number of studies. While the residual approach attempts to capture the effect of innovation on spending, it may be the case that innovations are not quality improving. The positive result on the number of QALYs is both reassuring as a separate proxy of innovation, but also provides some rough evidence that spending growth is correlated with higher quality treatments.15
The fourth column is the same as column (3) but includes the average cost change from new innovations. We find the cost of new treatments to be highly significant. This is reassuring and suggests that when a condition has relatively high-cost innovations (as measured in the cost-effectiveness data) that this shows up in higher spending growth in the HCSA.
Finally, it may be the case that quality across studies may be additive. For example, if each observation in the CEAR data was for a separate new innovation. In specification (5) we include both an average QALY measure and a total QALY measure, which adds up QALYs across studies, and we find the total QALY measure is statistically significant, while the average QALY change is not. This provides some suggestive evidence that QALY gains reported across multiple studies may be more important than just the average QALY gain.16 Similarly, costs may also be additive. In column (6) we include the total and average cost change and find the total cost change and total QALY change to be statistically significant. While we chose to focus on the number of studies as the preferred proxy for innovation, it is worth noting that using QALYs as a proxy for innovation produces very similar results. In particular, the specification in column (5) of Table 5 implies that innovation accounts for about 15 percent of spending growth.
Decomposition of Spending Growth into Treated Prevalence and Spending-per-case
Another related question is whether this spending growth is driven by spending per case or by the number of treated cases (Chernew and Newhouse (2011)), which we analyze in more detail in appendix section B. If spending growth is driven primarily through an increase in spending per case, then this suggests that technology may be driving spending growth primarily through high cost treatments. Across several specifications, we find no consistent evidence that innovation only affects spending per case or treated prevalence. A potential explanation may be that technologies have unique effects depending on the condition. For example, rheumatoid arthritis drugs introduced over this period were very costly, and likely drove the spending per case up. Alternatively, the diffusion of improved anti-cholesterol drugs potentially drove up treated prevalence over this period as more people are coded as having high cholesterol, which could have reduced the average spending per case of cholesterol over time. Anti-cholesterol drugs may also have reduced costly heart disease, also reducing spending per case.
Table 5: Regression of Spend 5-Year Growth Rate on Cost, QALY and Proxies of Innovation
| (1) | (2) | (3) | (3) | (4) | (5) | (6) |
| Log(Num Studies+1) | 0.0224∗∗ | 0.0185∗∗ | 0.0134 | |||
| (0.00961) | (0.00923) | (0.00904) | ||||
| Other Log(Num | 0.0237∗ | 0.0251∗∗ | 0.0240∗∗ | 0.0228∗ | 0.0227∗ | 0.0222∗ |
| Studies+1) | (0.0122) | (0.0124) | (0.0122) | (0.0121) | (0.0121) | (0.0121) |
| Avg. Cost Change | 0.0704∗∗∗ | 0.00431 | ||||
| (0.0267) | (0.0250) | |||||
| Avg. QALY Change | 0.0385∗∗ | 0.0285 | 0.0261 | 0.00387 | 0.00456 | |
| (0.0183) | (0.0175) | (0.0173) | (0.0180) | (0.0178) | ||
| Tot. QALY Change | 0.00848∗∗∗ | 0.00686∗∗∗ | ||||
| (0.00214) | (0.00209) | |||||
| Total Cost Change | 0.0139∗∗∗ | |||||
| (0.00514) | ||||||
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.027 | 0.025 | 0.030 | 0.034 | 0.034 | 0.040 |
Note: The table shows results from regressions of spending growth per capita on proxies of innovation. In addition to the proxies of innovation based on study counts, the table reports alternative proxies based on changes in QALYs and costs of innovations, as reported in studies in the CEAR database. Standard errors are in parentheses and are clustered by CCS Condition Category.
While the effect of innovation on spending per case and treated prevalence may be idiosyncratic, we do find that the relationship between the CEAR measured incremental treatment cost of a new innovation is statistically significantly related to the average spending per case measured in the HCSA, as shown in appendix Table A6. The incremental cost of a new innovation does not affect the treated prevalence, as shown in appendix Table A7. This suggests that the CEAR data can separate costly new innovations from low-cost innovations or cost-reducing innovation.
Discussion
This paper provides two contributions. First, it provides new evidence of the role that innovation has on spending growth. Prior research in this area measures innovation through a residual. The residual approach relies on the assumption that all unexplained growth in spending is driven by technology. However, factors such as inefficiency, market power, and structural changes in the health care system may be difficult to account for in the aggregate residual. We construct a more direct proxy for innovation at the condition- level and we find a strong association between our innovation proxy and spending growth. Importantly, our identification strategy controls for year fixed-effects, which directly account for all unobserved factors that affect spending that might have a common effect across disease conditions (e.g., income, demographics, insurance, prices, and population health, as well as inefficiencies, market power, and structural changes in the health systems).
The second contribution is that we use our proxy for innovation to provide a unique estimate of the contribution of innovation on spending growth. We show that around 18 percent of spending growth is attributable to new innovations. This is likely a lower bound on the true share of spending growth attributable to innovation for a couple of reasons. First, there are arguably technological advances that are common across conditions (e.g., MRIs and other diagnostic technology), which will be removed with the inclusion of year-specific dummy variables. Second, using cost-effectiveness studies as a proxy for innovation is imperfect, potentially leading to attenuation bias lowering the magnitude of the estimated contribution of innovation to spending, relative to the actual contribution.
Given the relatively limited time horizon and changes in the cost-effectiveness database over time, it is not possible to examine whether the role of technology in affecting spending is increasing or decreasing over time, as is analyzed in Smith et al. (2022).
Conclusion
Our paper provides new supporting evidence for the broadly held view that medical innovation is a key driver of spending growth. Applying a unique approach to investigate this question, we find that those conditions where more cost-effectiveness studies are conducted, experience significantly more spending growth. We find that our proxy for innovation accounts for around 18 percent of growth in spending per capita, which is likely a lower bound for the contribution of innovation on spending.
This result has important implications for measurement and welfare, as it suggests that a substantial portion of the spending growth is driven by new technologies that might improve treatment outcomes, but which also drive spending higher. This finding suggests that to better understand productivity and welfare generated by the health sector, it will be important to quantify both the welfare benefits and costs from new medical technologies.
Footnotes
1Related to this approach, some papers have attempted to capture forces that drive technological progress, but this is also measured at an aggregate national level.
2The most recent study, Smith et al. (2022), finds share attributable to technology is around 30 percent.
3For example, diagnostic technology or the adoption of electronic medical records may help in the treatment of many conditions, but these innovations would not be accounted for in our estimates as they would be captured by our year fixed effects.
4A QALY unit accounts for both mortality and quality of life. One QALY indicates one year of life in perfect health.
5The breakdown of observations in the CEAR database are the following: We begin with 7,287 CEAR articles. Exactly 871 articles were dropped due to missing disease information, another 408 were dropped due to irreconcilable disagreements between two Tufts condition mapping methodologies, 1,068 articles were dropped due to missing QALY information, and 174 articles were dropped for being outside the sample period.
We obtain very similar results if the 1,068 articles that are missing QALYs are added back into the main analysis. However, we drop those articles in our preferred specification so that our estimates using the QALYs as a proxy for innovation uses a consistent sample.
6Treated prevalence is measured as spending per capita divided by spending per case.
7Often the difference in CCS condition categories assigned by the two methods of mapping is similar, such as “diabetes without complications” and “diabetes with complications.”
8As an example, suppose conditions D1, D2, and D3 are all in the same AHRQ disease category. Let , and be the number of studies observed for each of these conditions. In this case, the spillover for and are calculated as , , and , respectively.
9It is challenging to link to new technologies in the preventative medicine category and the category of “residual codes.” For this reason, we drop these categories in some of our robustness checks.
10For example, we do not know if the treatment is relevant for a small or large population. We use the number of studies as our proxy rather than QALYs, as it is less skewed and can more easily be normalized to account for changes in the number of studies over time.
11The MEPS sample size is too small to estimate spending by condition by year and leads to noisy estimates Dunn et al. (2015).
12Similar results are obtained when a 5-year initial growth rate is included.
13Spending by condition is highly skewed, by applying weights on the log of spending, this weights higher cost conditions more.
14We obtain similar results when estimating on the full sample covering the time-period from 2000 to 2017 (see Table A2.)
15In appendix table A3, we recreate table 3, but using QALYs as our measure of innovation. Results are not as robust as in Table 3, but most specifications are still positive and significant.
16This may be due to multiple innovations, or the additional studies may provide greater confidence in the QALY gains of a specific treatment.
References
Chandra, A., J. Holmes, and J. Skinner (2013). Is this time different? the slowdown in healthcare spending. Technical report, National Bureau of Economic Research.
Chernew, M., A. M. Fendrick, and R. A. Hirth (1997). Managed care and medical technology: implications for cost growth. Health Affairs 16 (2), 196–206.
Chernew, M. E. and J. P. Newhouse (2011). Health care spending growth. In Handbook of health economics, Volume 2, pp. 1–43. Elsevier.
Curtiss, F. R. (2005). Who needs xr, la, sr, xl, er, or cr? Journal of Managed Care Pharmacy 11 (9).
Cutler, D. M. (1995). Technology, health costs, and the nih. Unpublished paper prepared for NIH Roundtable on Economics.
Cutler, D. M., K. Ghosh, K. L. Messer, T. Raghunathan, A. B. Rosen, and S. T. Stewart (2022). A satellite account for health in the United States. American Economic Review 112 (2), 494–533.
Cutler, D. M., K. Ghosh, K. L. Messer, T. E. Raghunathan, S. T. Stewart, and A. B. Rosen (2019). Explaining the slowdown in medical spending growth among the elderly, 1999–2012. Health Affairs 38 (2), 222–229.
Dauda, S., A. Dunn, and A. Hall (2022). A systematic examination of quality-adjusted price index alternatives for medical care using claims data. Journal of Health Economics 85, 102662.
Dunn, A., A. Hall, and S. Dauda (2022). Are medical care prices still declining? a re- examination based on cost-effectiveness studies. Econometrica 90 (2), 859–886.
Dunn, A., L. Rittmueller, and B. Whitmire (2015). Introducing the new BEA health care satellite account. Survey of Current Business 95 (1), 1–21.
Dunn, A., L. Rittmueller, and B. Whitmire (2016). Health care spending slowdown from 2000 to 2010 was driven by lower growth in cost per case, according to a new data source. Health Affairs 35 (1), 132–140.
Dunn, A., B. Whitmire, A. Batch, L. Fernando, and L. Rittmueller (2018). High spending growth rates for key diseases in 2000–14 were driven by technology and demographic factors. Health Affairs 37 (6), 915–924.
Dynan, K. and L. Sheiner (2018). GDP as a measure of economic well-being. Technical report, Hutchins Center Working Paper.
Eggleston, K., B. K. Chen, C.-H. Chen, Y. I. Chen, T. Feenstra, T. Iizuka, J. T. Lam, G. M. Leung, J.-f. R. Lu, B. Rodriguez-Sanchez, et al. (2019). Are quality-adjusted medical prices declining for chronic disease? evidence from diabetes care in four health systems. Technical report, National Bureau of Economic Research.
Fojo, T., S. Mailankody, and A. Lo (2014). Unintended consequences of expensive cancer therapeutics—the pursuit of marginal indications and a me-too mentality that stifles innovation and creativity. JAMA Otolaryngol Head Neck Surg 140 (12).
Gastala, N. M., P. Wingrove, A. Gaglioti, S. Petterson, and A. Bazemore (2016). Medicare part d: Patients bear the cost of ‘me too’ brand-name drugs. Health Affairs 35 (7).
Giugliano, R. P., T. R. Pedersen, J. L. Saver, P. S. Sever, A. C. Keech, E. A. Bohula, S. A. Murphy, S. M. Wasserman, N. Honarpour, H. Wang, A. L. Pineda, and M. S. Sabatine (2020). Stroke prevention with the pcsk9 (proprotein convertase subtilisinkexin type 9) inhibitor evolocumab added to statin in high-risk patients with stable atherosclerosis. Stroke 51 (5).
Hall, A. E. (2017). Adjusting the measurement of the output of the medical sector for quality: A review of the literature. Medical Care Research and Review 74 (6), 639–667.
Hemphill, C. S. and B. N. Sampat (2012). Evergreening, patent challenges, and effective market life in pharmaceuticals. Journal of Health Economics 31 (2).
Highfill, T. and E. Bernstein (2019). Using disability adjusted life years to value the treatment of thirty chronic conditions in the us from 1987 to 2010: a proof of concept. International journal of health economics and management 19 (3-4), 449–466.
Matsumoto, B. et al. (2021). Producing Quality Adjusted Hospital Price Indexes. US Department of Labor, U.S. Bureau of Labor Statistics, Office of Prices and Index Number Research, Working Paper.
Newhouse, J. P. (1992). Medical care costs: how much welfare loss? Journal of Economic perspectives 6 (3), 3–21.
Olek, M. J. and D. Mowry (2015). Medicare drug spending dashboard. The Centers for Disease Control and Prevention Fact Sheet .
Olek, M. J. and D. Mowry (2022). Initial disease-modifying therapy for relapsing-remitting multiple sclerosis in adults. Up to Date.
Ridker, P. M., E. Danielson, F. A. Fonseca, G. J. A. M. Genest, Jacques and, J. J. Kastelein,
- Koenig, L. A. J. Libby, Peter and, J. G. MacFadyen, B. G. Nordestgaard, J. Shepherd,
- T. Willerson, and R. J. Glynn (2008). Rosuvastatin to prevent vascular events in men and women with elevated c-reactive protein. New England journal of medicine 359 (21).
Romley, J. A., A. Dunn, D. Goldman, and N. Sood (2020, January). Quantifying Productivity Growth in the Delivery of Important Episodes of Care Within the Medicare Program Using Insurance Claims and Administrative Data. University of Chicago Press.
Schwartz, W. B. (1987). The inevitable failure of current cost-containment strategies: why they can provide only temporary relief. JAMA 257 (2), 220–224.
Sheiner, L. and A. Malinovskaya (2016). Measuring productivity in healthcare: an analysis of the literature. Hutchins center on fiscal and monetary policy at Brookings.
Smith, S., J. P. Newhouse, and M. S. Freeland (2009). Income, insurance, and technology: why does health spending outpace economic growth? Health affairs 28 (5), 1276–1284.
Smith, S. D., J. P. Newhouse, and G. A. Cuckler (2022, December). Health care spending growth has slowed: Will the bend in the curve continue? Working Paper 30782, National Bureau of Economic Research.
Solow, R. M. (1957). Technical change and the aggregate production function. The review of Economics and Statistics, 312–320.
Tabernero, J. (2015). Proven efficacy, equitable access, and adjusted pricing of anti-cancer therapies: no ‘sweetheart’ solution. Annals of Oncology 26 (8).
Tice, J., K. Kuntz, K. Wherry, R. Chapman, M. Seidner, S. Pearson, and D. Rand (2020). Modulator treatments for cystic fibrosis: Effectiveness and value. Institute For Clinical and Economic Review .
van der Gronde, T., C. A. Uyl-de Groot, and T. Pieters (2017). Addressing the challenge of high-priced prescription drugs in the era of precision medicine: A systematic review of drug life cycles, therapeutic drug markets and regulatory frameworks. PloS one 12 (8).
Weaver, M. R., J. Joffe, M. Ciarametaro, R. W. Dubois, A. Dunn, A. Singh, G. W. Sparks,
- Stafford, C. J. Murray, and J. L. Dieleman (2022). Health care spending effective- ness: Estimates suggest that spending improved us health from 1996 to 2016. Health Affairs 41 (7), 994–1004.
Appendix A
Growing Sample Size in CEAR Data and Normalization of the Number of Studies
Table A1 provides some basic descriptive statistics of key variables for the years 2005, 2010 and 2015. The first column shows the distribution of the 5-year growth rate. The second column shows the average of the number of studies. The third column shows the average number of spillover studies. The spending growth slows down considerably over this time period, which is a point noted previously in Chandra et al. (2013), Dunn et al. (2016), and Cutler et al. (2019) as well as others. The other notable feature is that the number of studies reported changes considerably over time, with more studies observed in recent years of the sample.
The growth in sample size has little effect on the main results, as the analysis focuses on the relative growth across condition categories.
Demographic Control Variable
One variable that may be unique to each condition includes demographic factors such as age and sex. For instance, the aging of the population may have a larger effect on circulatory conditions, relative to conditions related to pregnancy. Adding an age variable directly into our regression model for each condition is not possible because there would be too many covariates (e.g., average population age interacted with each condition category). Because adding an age variable would yield excessive covariates, we apply a methodology that at- tempts to capture the growth in spending for each condition solely due to changes in the age-sex composition of the population.
Table A1: Descriptive Statistics on the Growth Rates and Number of Studies by Year
| Five-Year Growth Rate | Num. of Studies | Num. | of Spillover Studies | |
| 2005 | ||||
| mean | 0.183 | 1.496 | 1.339 | |
| sd | 0.276 | 3.432 | 1.913 | |
| p10 | -0.124 | 0 | 0 | |
| p90 | 0.491 | 5 | 3.250 | |
| 2010 | ||||
| mean | 0.113 | 4.142 | 3.705 | |
| sd | 0.211 | 9.361 | 5.897 | |
| p10 | -0.111 | 0 | 0 | |
| p90 | 0.363 | 12 | 7.900 | |
| 2015 | ||||
| mean | 0.104 | 6.876 | 6.407 | |
| sd | 0.259 | 14.69 | 8.865 | |
| p10 | -0.119 | 0 | 0 | |
| p90 | 0.446 | 19 | 13 |
Note: This table shows descriptive statistics for the key variables of analysis across three years, 2005, 2010 and 2015. These estimates remove the outlier growth rates that exceed 200 percent over a five-year period. The figure shows several patterns: (1) there is a large degree of variation across all the key variables. The mean growth rate in spending is positive across all years, but there is great variation within any year. The table also shows that the growth rate is positive but declining relative to 2005. The number of studies is increasing over this time-period, primarily due to the growth in the number of observations in the CEAR database, but the key estimates are not dependent on the growth in observations over time, as they include year fixed effects.
Specifically, we use the Medical Expenditure Panel Survey (MEPS) data, which has detailed information on spending by disease condition. We divide the population into age- sex buckets (e.g., 0-18 and female; 0-18 and male; 19-40 and female; 19-40 and male, etc). Next, we calculate the average spending by CCS medical condition for each age-sex category over the entire period from 2000 to 2019. Although the MEPS sample size is relatively small with just 30,000 individuals each year, to construct our control variable we are able to average over 19 years of data, obtaining a relatively large sample. Importantly, the spending by CCS is averaged over all years of data, so it does not vary over time. Next, we calculate the share of the population in each age-sex bucket in each year. Finally, we combine average spending by age-sex-CCS category with the share of the population in each age-sex category across years by constructing a population weighted average of spending in each year. More precisely, we multiply the population share in each demographic bucket in each year by the average spending by CCS for each demographic bucket. This produces an estimate of spending by disease and year, where the change in spending is entirely driven by the change in the population shares. Using age-sex demographics aggregated across conditions, we find that spending growth increases by 9.5 percent over the period from 2000-2015 solely due to demographic changes.
Additional Regression Results
Table A2: Regression of 5-Year Spending Growth Rates on Counts of the Number of Studies and Studies in Related Categories: Full Sample
| Model Description | Baseline | No Demo. | Controls | Cont. & Trend | IV | Weighted |
|
Single Proxy |
||||||
| Spend | Spend | Spend | Spend | Spend | Spend | |
| Log(Num Studies+1) | 0.0218∗∗ | 0.0191∗∗ | 0.0240∗∗ | 0.0127 | 0.0571∗∗∗ | 0.0207∗∗ |
| (0.00992) | (0.00961) | (0.0111) | (0.00971) | (0.0178) | (0.00985) | |
| Observations | 3385 | 3385 | 3385 | 3385 | 3385 | 3385 |
| Adjusted R2 | 0.018 | 0.016 | 0.108 | 0.199 | . | 0.019 |
| Two Proxies | ||||||
| Log(Num Studies+1) | 0.0206∗∗ | 0.0171∗ | 0.0258∗∗ | 0.0144∗∗∗ | 0.0545∗∗∗ | 0.0197∗∗ |
| (0.00977) | (0.00942) | (0.0115) | (0.00469) | (0.0172) | (0.00972) | |
| Other Log(Num | 0.0233∗ | 0.0189∗ | 0.0193 | 0.0169∗∗∗ | 0.0205∗ | 0.0230∗ |
| Studies+1) | (0.0119) | (0.0111) | (0.0140) | (0.00643) | (0.0121) | (0.0118) |
| Observations | 3385 | 3385 | 3385 | 3385 | 3385 | 3385 |
| Adjusted R2 | 0.023 | 0.020 | 0.110 | 0.200 | 0.003 | 0.024 |
| Single Proxy – Normalized | ||||||
| Log(Num Studies+1) | 0.0214∗∗ | 0.0190∗∗ | 0.0249∗∗ | 0.0145∗ | 0.0372∗∗∗ | 0.0204∗∗ |
| (0.00860) | (0.00836) | (0.00964) | (0.00809) | (0.0125) | (0.00856) | |
| Observations | 3385 | 3385 | 3385 | 3385 | 3385 | 3385 |
| Adjusted R2 | 0.020 | 0.018 | 0.111 | 0.200 | 0.014 | 0.021 |
|
Two Proxies – Normalized |
||||||
| Log(Num Studies+1) | 0.0204∗∗ | 0.0171∗∗ | 0.0276∗∗∗ | 0.0169∗∗∗ | 0.0349∗∗∗ | 0.0197∗∗ |
| (0.00850) | (0.00821) | (0.00992) | (0.00414) | (0.0126) | (0.00848) | |
| Other Log(Num | 0.0243∗∗ | 0.0198∗∗ | 0.0245∗ | 0.0213∗∗∗ | 0.0234∗∗ | 0.0239∗∗ |
| Studies+1) | (0.0104) | (0.00969) | (0.0127) | (0.00572) | (0.0104) | (0.0103) |
| Observations | 3385 | 3385 | 3385 | 3385 | 3385 | 3385 |
| Adjusted R2 | 0.028 | 0.024 | 0.115 | 0.203 | 0.023 | 0.029 |
Note: All spending growth is adjusted for economy-wide inflation using the GDP index. The table shows results from regressions of spending growth per capita on proxies of innovation based on the counts of the number of studies. The regression covers the full sample period from 2000 to 2017, including the discontinuity created by the change in ICD9 to ICD10 coding in 2015. All regressions include year fixed effects. The columns differ by the covariates included in the specification, with a description in the top column. The baseline specification includes the demographic covariate, second column excludes the demographic covariate, the third column includes additional controls, and the fourth column includes additional controls and the initial 3-year growth rate of the condition. The fifth column applies an IV estimation, where the IV is the average QALY from cost-effectiveness studies over the past five years. The sixth column is the baseline model where the regression is weighted by the log of the average spending. The specification also differs by panel. The first panel includes a single proxy for innovation and the second panel includes two proxies. The last two panels repeat the first two panels, but the number of studies is normalized across years. Standard errors are in parentheses and are clustered by CCS Condition Category.
Table A3: Regression of 5-Year Spending Growth Rates on QALYs
| Model Description | Baseline | No Demo. | Controls | Cont. & Trend | Weighted |
|
Avg QALY |
|||||
| Avg. QALY Change | 0.0385∗∗ | 0.0385∗∗ | 0.0242 | -0.00302 | 0.0385∗∗ |
| (0.0183) | (0.0183) | (0.0164) | (0.0164) | (0.0180) | |
| Other Log(Num | 0.0251∗∗ | 0.0251∗∗ | 0.0156 | 0.0149 | 0.0244∗∗ |
| Studies+1) | (0.0124) | (0.0116) | (0.0136) | (0.0119) | (0.0123) |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.025 | 0.025 | 0.115 | 0.244 | 0.027 |
|
Total QALY |
|||||
| Tot. QALY Change | 0.00883∗∗∗ | 0.00878∗∗∗ | 0.00616∗∗∗ | 0.000536 | 0.00874∗∗∗ |
| (0.00223) | (0.00225) | (0.00236) | (0.00247) | (0.00223) | |
| Other Log(Num | 0.0226∗ | 0.0220∗ | 0.0166 | 0.0151 | 0.0219∗ |
| Studies+1) | (0.0121) | (0.0114) | (0.0138) | (0.0119) | (0.0120) |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.034 | 0.035 | 0.119 | 0.244 | 0.037 |
Note: The table shows results from regressions of spending growth per capita on proxies of innovation based on QALYs from the CEAR database. All spending growth is adjusted for economy-wide inflation using the GDP index. All regressions include year fixed effects. The columns differ by the covariates included in the specification, with a description in the top column. The baseline specification includes the demographic covariate, second column excludes the demographic covariate, the third column includes additional controls, and the fourth column includes additional controls and the initial 3-year growth rate of the condition. The fifth column is the baseline model where the regression is weighted by the log of the average spending. The specification also differs by panel. The first panel includes a single proxy for innovation and the second panel includes two proxies. The last two panels repeat the first two panels, but the number of studies is normalized across years. Standard errors are in parentheses and are clustered by CCS Condition Category.
Appendix B Decomposition of Spending Growth into Treated Prevalence and Spending-per-case
In this section we explore using spending per case and treated prevalence as outcome variables. Table A4 presents the results where spending per case is the outcome, while Table A5 presents the results with treated prevalence as the outcome. We see almost no effect on the spending per case. For treated prevalence, we see some positive and significant impacts, but these are not as robust as the main results using total spending growth. Tables A6 and A7 repeat these analyses using the incremental cost and QALY estimates as regressors. One notable finding is that the average cost variable constructed from the CEAR data is highly correlated with the spending per case in the HCSA data. Otherwise, we find few significant impacts, except on the amount of spillover studies.
Table A4: Regression of 5-Year Spending Per Case Growth Rates on Counts of the Number of Studies and Studies in Related Categories
| Model Description | Baseline | No Demo. | Controls | Cont. & Trend | IV | Weighted |
|
Single Proxy |
||||||
| Per Case Spend | Per Case Spend | Per Case Spend | Per Case Spend | Per Case Spend | Per Case Spend | |
| Log(Num Studies+1) | 0.00402 | -0.00225 | 0.0125 | 0.00952 | 0.0318∗ | 0.00384 |
| (0.00824) | (0.00833) | (0.0105) | (0.00970) | (0.0176) | (0.00807) | |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.005 | 0.000 | 0.017 | 0.021 | -0.003 | 0.006 |
| Two Proxies | ||||||
| Log(Num Studies+1) | 0.00382 | -0.00207 | 0.0118 | 0.00881 | 0.0314∗ | 0.00369 |
| (0.00828) | (0.00855) | (0.0109) | (0.0101) | (0.0176) | (0.00808) | |
| Other Log(Num | 0.00571 | -0.00186 | -0.00621 | -0.00680 | 0.00412 | 0.00527 |
| Studies+1) | (0.00987) | (0.00891) | (0.00960) | (0.00967) | (0.00973) | (0.00936) |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.005 | -0.000 | 0.017 | 0.021 | -0.003 | 0.006 |
| Single Proxy – Normalized | ||||||
| Log(Num Studies+1) | 0.00367 | -0.00142 | 0.0110 | 0.00833 | 0.0124 | 0.00362 |
| (0.00687) | (0.00695) | (0.00871) | (0.00795) | (0.0122) | (0.00671) | |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.005 | 0.000 | 0.017 | 0.021 | 0.004 | 0.006 |
|
Two Proxies – Normalized |
||||||
| Log(Num Studies+1) | 0.00349 | -0.00146 | 0.0108 | 0.00805 | 0.0118 | 0.00350 |
| (0.00687) | (0.00711) | (0.00910) | (0.00830) | (0.0121) | (0.00670) | |
| Other Log(Num | 0.00738 | 0.000563 | -0.00154 | -0.00237 | 0.00705 | 0.00680 |
| Studies+1) | (0.00842) | (0.00749) | (0.00825) | (0.00813) | (0.00831) | (0.00797) |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.005 | -0.000 | 0.017 | 0.021 | 0.004 | 0.006 |
Note: The table shows results from regressions of spending growth per case on proxies of innovation based on the counts of the number of studies. All spending growth is adjusted for economy-wide inflation using the GDP index. All regressions include year fixed effects. The columns differ by the covariates included in the specification, with a description in the top column. The baseline specification includes the demographic covariate, second column excludes the demographic covariate, the third column includes additional controls, and the fourth column includes additional controls and the initial 3-year growth rate of the condition. The fifth column applies an IV estimation, where the IV is the average QALY from cost-effectiveness studies over the past five years. The sixth column is the baseline model where the regression is weighted by the log of the average spending. The specification also differs by panel. The first panel includes a single proxy for innovation and the second panel includes two proxies. The last two panels repeat the first two panels, but the number of studies is normalized across years. Standard errors are in parentheses and are clustered by CCS Condition Category.
Table A5: Regression of 5-Year Treated Prevalence Growth Rates on Counts of the Number of Studies and Studies in Related Categories
| Model Description | Baseline | No Demo. | Controls | Cont. & Trend | IV | Weighted |
|
Single Proxy |
||||||
| Treated Prev. | Treated Prev. | Treated Prev. | Treated Prev. | Treated Prev. | Treated Prev. | |
| Log(Num Studies+1) | 0.0127∗ | 0.0166∗∗ | 0.00442 | -0.00314 | 0.0169 | 0.0123∗ |
| (0.00722) | (0.00707) | (0.00800) | (0.00752) | (0.0134) | (0.00710) | |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.013 | 0.011 | 0.093 | 0.129 | 0.013 | 0.014 |
| Two Proxies | ||||||
| Log(Num Studies+1) | 0.0117 | 0.0137∗ | 0.00634 | -0.00136 | 0.0142 | 0.0115 |
| (0.00731) | (0.00717) | (0.00814) | (0.00759) | (0.0144) | (0.00720) | |
| Other Log(Num | 0.0286∗∗∗ | 0.0312∗∗∗ | 0.0185 | 0.0170∗ | 0.0285∗∗∗ | 0.0272∗∗∗ |
| Studies+1) | (0.0107) | (0.00973) | (0.0118) | (0.00986) | (0.0108) | (0.0103) |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.020 | 0.020 | 0.094 | 0.130 | 0.020 | 0.021 |
| Single Proxy – Normalized | ||||||
| Log(Num Studies+1) | 0.0114∗ | 0.0146∗∗ | 0.00522 | -0.00165 | 0.0139 | 0.0110∗ |
| (0.00637) | (0.00627) | (0.00705) | (0.00653) | (0.0123) | (0.00625) | |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.014 | 0.011 | 0.093 | 0.129 | 0.014 | 0.015 |
|
Two Proxies – Normalized |
||||||
| Log(Num Studies+1) | 0.0107∗ | 0.0122∗ | 0.00748 | 0.000417 | 0.0117 | 0.0106∗ |
| (0.00645) | (0.00635) | (0.00719) | (0.00666) | (0.0132) | (0.00633) | |
| Other Log(Num | 0.0265∗∗∗ | 0.0285∗∗∗ | 0.0199∗∗ | 0.0178∗∗ | 0.0265∗∗∗ | 0.0253∗∗∗ |
| Studies+1) | (0.00931) | (0.00840) | (0.0100) | (0.00818) | (0.00929) | (0.00890) |
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | 2868 |
| Adjusted R2 | 0.022 | 0.022 | 0.096 | 0.131 | 0.022 | 0.023 |
Note: The table shows results from regressions of treated prevalence per capita on proxies of innovation based on the counts of the number of studies. All regressions include year fixed effects. The columns differ by the covariates included in the specification, with a description in the top column. The baseline specification includes the demographic covariate, second column excludes the demographic covariate, the third column includes additional controls, and the fourth column includes additional controls and the initial 3-year growth rate of the condition. The fifth column applies an IV estimation, where the IV is the average QALY from cost-effectiveness studies over the past five years. The sixth column is the baseline model where the regression is weighted by the log of the average spending. The specification also differs by panel. The first panel includes a single proxy for innovation and the second panel includes two proxies. The last two panels repeat the first two panels, but the number of studies is normalized across years. Standard errors are in parentheses and are clustered by CCS Condition Category.
Table A6: Regression of Spending Per Case 5-Year Growth Rate on Cost, QALY and Proxies of Innovation
| (1) | (2) | (3) | (3) | (4) | (5) | (6) |
| Log(Num Studies+1) | 0.00382 | 0.00250 | -0.00235 | |||
| (0.00828) | (0.00804) | (0.00718) | ||||
| Other Log(Num | 0.00571 | 0.00595 | 0.00580 | 0.00474 | 0.00424 | |
| Studies+1) | (0.00987) | (0.00977) | (0.00981) | (0.00970) | (0.00951) | |
| Avg. Cost Change | 0.0659∗∗ | |||||
| (0.0274) | ||||||
| Avg. QALY Change | 0.0110 | 0.00966 | 0.00742 | -0.0144 | ||
| (0.0146) | (0.0140) | (0.0139) | (0.0162) | |||
| Tot. QALY Change | 0.00624∗∗ | |||||
| (0.00286) | ||||||
| Total Cost Change | ||||||
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | |
| Adjusted R2 | 0.005 | 0.005 | 0.005 | 0.007 | 0.008 |
Note: The table shows results from regressions of spending growth per case on proxies of innovation. All spending growth is adjusted for economy-wide inflation using the GDP index. In addition to the proxies of innovation based on study counts, the table reports alternative proxies based on changes in QALYs and costs of innovations, as reported in studies in the CEAR database. Standard errors are in parentheses and are clustered by CCS Condition Category.
Table A7: Regression of Treated Prevalence 5-Year Growth Rate on Cost, QALY and Proxies of Innovation
| (1) | (2) | (3) | (3) | (4) | (5) | (6) |
| Log(Num Studies+1) | 0.0117 | 0.0101 | 0.0103 | |||
| (0.00731) | (0.00710) | (0.00734) | ||||
| Other Log(Num | 0.0286∗∗∗ | 0.0293∗∗∗ | 0.0287∗∗∗ | 0.0288∗∗∗ | 0.0289∗∗∗ | |
| Studies+1) | (0.0107) | (0.0107) | (0.0107) | (0.0108) | (0.0108) | |
| Avg. Cost Change | -0.00348 | |||||
| (0.0176) | ||||||
| Avg. QALY Change | 0.0172 | 0.0118 | 0.0119 | 0.0108 | ||
| (0.0131) | (0.0125) | (0.0125) | (0.0155) | |||
| Tot. QALY Change | 0.00155 | |||||
| (0.00282) | ||||||
| Total Cost Change | ||||||
| Observations | 2868 | 2868 | 2868 | 2868 | 2868 | |
| Adjusted R2 | 0.020 | 0.019 | 0.020 | 0.020 | 0.019 |
Note: The table shows results from regressions of treated prevalence growth per capita on proxies of innovation. In addition to the proxies of innovation based on study counts, the table reports alternative proxies based on changes in QALYs and costs of innovations, as reported in studies in the CEAR database. Standard errors are in parentheses and are clustered by CCS Condition Category.
1Related to this approach, some papers have attempted to capture forces that drive technological progress, but this is also measured at an aggregate national level.